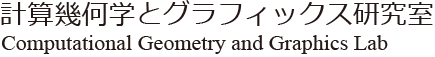ねじり折りのパラメトリックな変形 >ENG
概要
折り紙の技術は,収縮・展開する機構としての応用が期待されている.宇宙工学や医療工学,建築などの幅広い分野では,特定の条件を満たす折り紙の構造を実現するために,パラメトリックに変形できる折り紙のモデルが提案されている.これらのモデルの多くは,スケールを無視して特性を議論できるため,異なる分野への応用が可能である.そのための課題として,統一的なモデル,すなわち,各モデルを内包し,パラメトリックに変形可能なものの提案が挙げられる.本研究では,ねじり折りと呼ばれる折り線の集合のパラメトリックな作図・変形方法を提案する.そして,既存の大多数のモデルを内包する平坦折り可能な展開図を,ねじり折りの集合として一般化する方法を提案する.これにより、平坦折り可能な展開図を対象とした,ねじり折りを単位とした構造や,パラメトリックな変形などの,統一的な議論が可能となる.
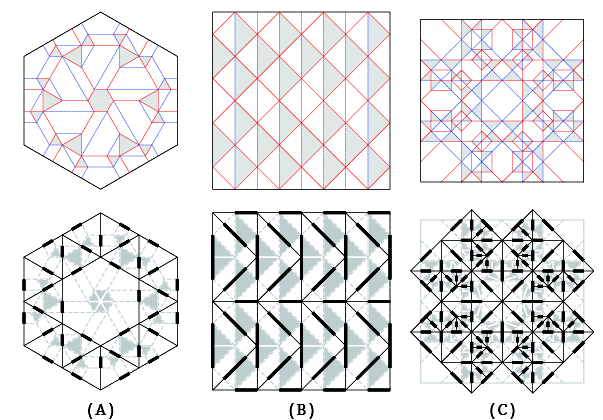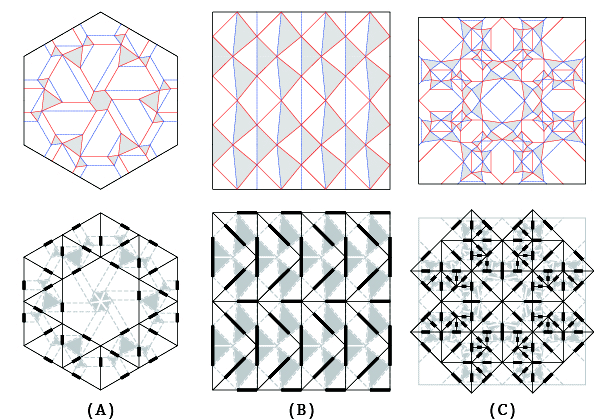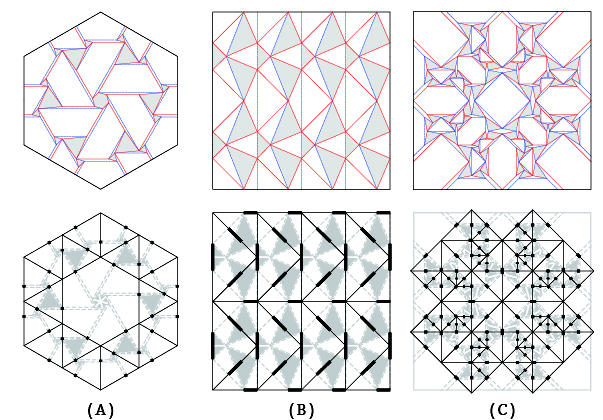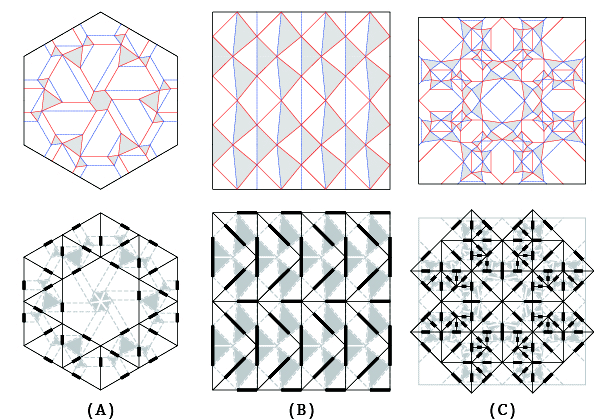
図01.ねじり折りを単位とするパラメトリックな変形の例
A:Roman Church Floor Tiling (designed by Eric Gjerde), B:吉村パターン, C:アジサイ折り
関連コンテンツ
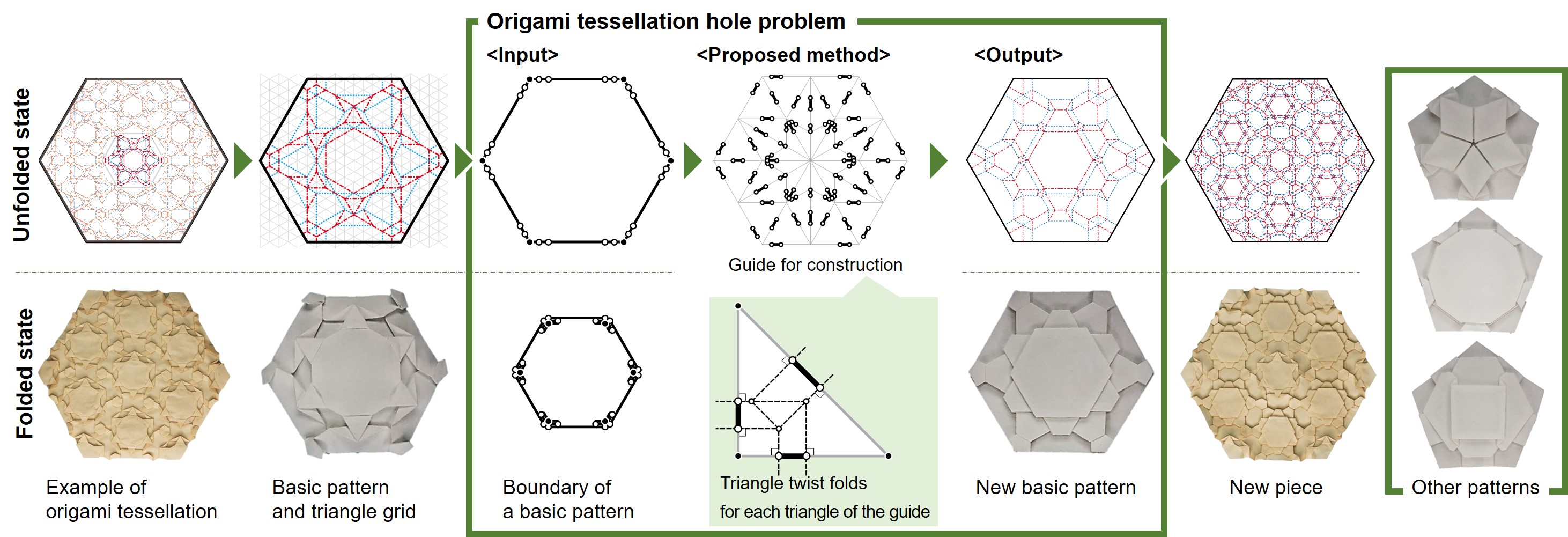
- Continuous deformation of flat-foldable crease patterns
via interpretation as set of twist-patterns- 本ページの内容を 論文としてまとめたもの
- TRIANGLE TWIST PATTERN MAKER
- 本ページで提案する作図法(ねじり作図法)を 支援するウェブアプリケーション
Index
平坦折り可能な展開図
- 本プロジェクトにおける(平坦折り可能な)展開図とは 次の折り線の集合を指す(図02)
- 「内部頂点周りの1つ飛ばしの内角の和が180°(川崎定理)」を満たす
- 境界を持つ場合 境界上の2点を結ぶ折り線を無視できる
- 明記の無い限り 折り線の「山折り」と「谷折り」を区別しない
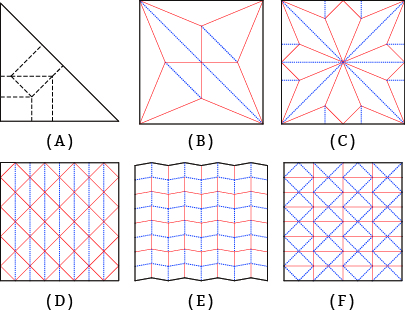
図02.平坦折り可能な展開図の一例
A:ねじり折り, B:ツルの基本形, C:カエルの基本形, D:吉村パターン, E:ミウラ折り, F:ナマコ折り
- 次の手順で得られる面の集合を 展開図の折りたたんだ状態と称する(図03)
- 面を節点 折り線を枝に見立てた全域木(全ての節点を通る木構造)を作る
- 根となる面を決める
- 葉に向かって枝を横断する度に その枝に対応する折り線で 枝から先の面を反転させる
- 折りたたんだ状態は 次の特徴を持つ
- 実際に折りたためた場合における 面のシルエットに相当する
- ある展開図の折りたたんだ状態は 並進・回転・反転によって一致する1種類に限られる
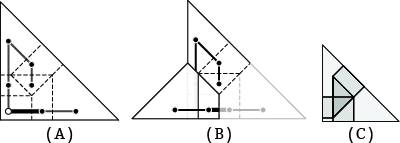
図03.図02Aから折りたたんだ状態を取得する流れ
A:全域木の決定, B:反転の例(Aの白点を根とし 太線で示す枝を対象としたもの), C:折りたたんだ状態
ねじり折り
- 「n角形の辺となる折り線と その辺の端点から同一の角度で延伸する折り線」からなる展開図を (n角形の)ねじり折りと呼称する(図04A)
- 中心面:中央のn角形
- プリーツ:各辺から延伸する2本1組の折り線
- ねじり角:プリーツと多角形の辺の成す角度
- ねじり折り同士は プリーツを共有することで 連結できる(図04B)
- 連結した結果 折り線同士が重複する場合 重複した折り線を除去したものも展開図のである(川崎定理を満たす)(図04C)
- n角形のねじり折りは 複数のねじり折りが 中心面の辺を重複させるように連結したものとみなせる(図05)
- 折りたたんだ状態を 異なるプリーツに囲まれた面を根として得た場合 中心面は ねじり角の2倍だけ回転したものとなる(連結した場合や重複した折り線が除去された場合も同様)
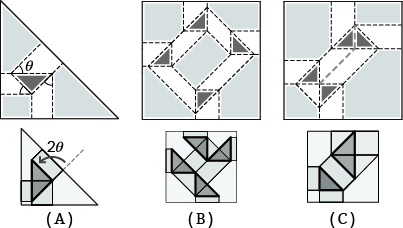
図04.ねじり折りの一例と (薄い灰色の面のいずれかを根とした)折りたたんだ状態
A:三角形のねじり折り, B:4つのねじり折りの連結, C:重複した折り線を有する ねじり折りの連結
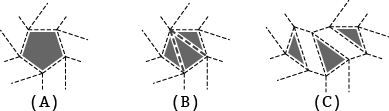
図05.五角形のねじり折り三角形のねじり折りの集合と解釈する流れ
A:五角形のねじり折り, B:重複し除去された折り線の復元, C:Bのプリーツの長さを長くした展開図
ねじり折りの作図・変形
- (連結された)ねじり折りは ねじり作図法と称した次の手順で作図できる(図06)
- 三角形のタイリングを作図する
- 各辺と同一直線上に 各辺を共通の比率で短くした線分(基準線)を配置する
- 基準線ごとに 各端点を通る垂直な2本の折り線(プリーツ)を作図する
- 三角形のタイルごとに プリーツの交点を折り線で結ぶことで 中心面を作図する
- 作図されたねじり折りは 次の特徴を持つ
- 川崎定理は保証されるが 折り線同士が交差する可能性がある
- 中心面と 作図に用いた三角形の面は 相似となる
- 折り線の重複と除去を許容し 境界上の2点を結ぶ折り線の無視を考慮すると 任意の展開図をねじり折りの集合として作図できる(詳細は ねじり折りを用いた展開図の一般化 で示す)
- タイリングと基準線の組み合わせをガイドと称する
- 作図の逆の手順により 三角形ねじり折りの集合からガイドを再構成できる
- ねじり折りは 三角形のねじり折りの集合とみなすことで ガイドを再構成できる
- ただし 再構成されるガイドは 三角形のタイリングの位置などに依存し 無数に考えられる
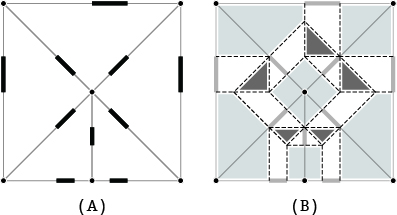
図06.ねじり折りの作図手順
A:ガイド(黒い太線が基準線), B:作図されたねじり折り
- ガイド中のパラメトリックな要素を変更することで 展開図を連続的に変形できる
- タイルの頂点
- 基準線の位置と長さ(図07)
- 基準線の長さや 対応する辺の形を変えても その辺と基準線における 始点間の距離と終点間の距離の比は一定とする
- 長さ0の基準線(
距離の比によって得られる 辺の内分or外分点)が 基準線の原点となる
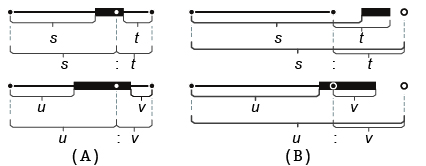
図07.s:t=u:vを満たすように 基準線の長さを2倍にする例と基準線の原点(白点)
A:基準線の原点が 辺の内分点となる例, B:基準線の原点が 辺の外分点となる例
- 基準線の長さを変えることで得られる展開図は 次の特徴を満たす(図08)
- 折り線の集合からなるグラフが 元々のものとグラフ同型である(折り線の繋がり方が一定である)
- 中心面は 回転しながら拡縮する
- 異なるプリーツに囲まれた面は 拡縮する(拡縮の中心は それらのプリーツに対応するガイドの辺が共有するガイドの頂点)
- 元々の折り線が交差しない場合 長さを0に近づけても折り線が交差しない
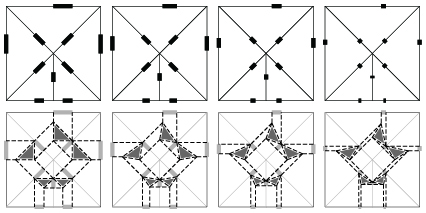
図08.図06から 基準線の長さを短くすることで得られる展開図
ねじり折りを用いた展開図の一般化
- 興味深いことに 展開図はねじり折りの集合とみなした一般化が可能である
- いいかえると 展開図から 次の手順に沿うことで ねじり折りの集合を再構成できる
- 折りたたまれた状態を取得する(図09A)
- 各面を元々の状態と折りたたまれた状態とで比較し 一致させるのに必要な変換で次の3種類に分類する
- ねじり面:回転変換と並進移動(図09B)
- 反転面:鏡映変換と並進移動
- 基礎面:並進移動 あるいは変換無し(根となる面)
- 各ねじり面から 同様の回転変換が施される中心面を持つねじり折り(以下の要素で構成されるもの)を再構成する(図09C,10)
- 中心面:ねじり面
- ねじり角:ねじり面に施された回転角の半分
- プリーツの長さ:任意の長さとする
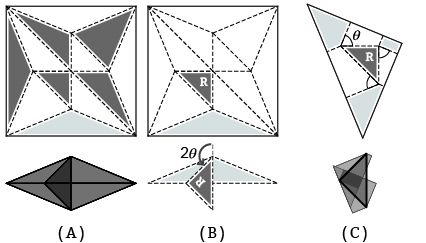
図09.A:ツルの基本形と折りたたんだ状態(濃い灰面:ねじり面,白面:反転面,薄い灰面:基礎面),
B:基礎面とねじり面R,C:ねじり面Rから再構成されたねじり折り
- 再構成されたねじり折り同士を 以下の事実に基づき可能な限り連結する(図10,11)
- 各ねじり面の辺は 必ず反転面と共有される
- ねじり面の辺から再構成されるプリーツの傾きは その辺を共有する反転面の他の辺から再構成されるものと一致する(図10)
- 再構成されたねじり折りは 反転面を挟んで反対側のねじり面から再構成されたねじり折りと プリーツを共有できる
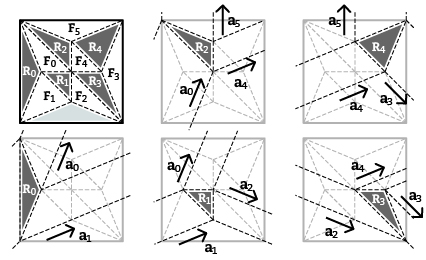
図10.図09Aに基づく各ねじり面Riから再構成されるねじり折り
プリーツの傾きaiは 反転面Fiに対応する
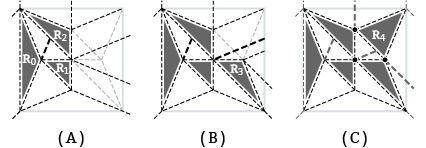
図11.図10に示す5種類のねじり面を連結する流れ(太線は 重複した折り線を示す)
A:ねじり折りR0,R1,R2の連結,B:Aとねじり折りR3の連結,C:Bとねじり折りR4の連結
- 再構成されたねじり折りの集合は 以下の操作を加えることで元々の展開図と一致するため 元々の展開図を ねじり折りで一般化したものとみなせる
- 重複した折り線を除去する
- 元々の展開図と同じ境界を定める
- 境界を結ぶ折り線は 無視できるものとする
- 展開図は 折りたたんだ状態に依存して 異なるねじり折りの集合とみなせる(図12)
- 追加の回転・鏡映変換が施された折りたたんだ状態も対象にできるため 再構成される集合は無数に考えられる
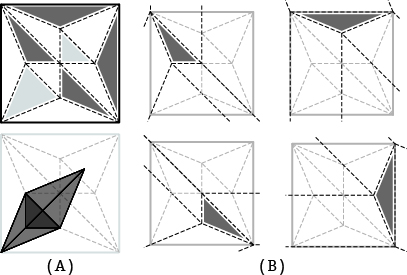
図12.A:図11のものと異なる面を根とした綿の分類,B:Aより再構成されるねじり折り
応用例
業績一覧
学術論文(査読有り)
- Yohei Yamamoto, Riku Nakazato, Jun Mitani, "Method for solving origami tessellation hole problem using triangle twist folding", Journal of Computational Design and Engineering, Vol.9, No.1, , pp 144-154, 2022[DOI:10.1093/jcde/qwab074]
- Yohei Yamamoto, Jun Mitani, "Shrinkable Self-Similar Structure Design", Journal of Mechanisms and Robotics, pp 1-10, 2022[DOI:10.1115/1.4053528]
- Yohei Yamamoto, Jun Mitani, "Continuous deformation of flat-foldable crease patterns via interpretation as set of twist-patterns", Journal of Computational Design and Engineering, 2023[DOI:10.1093/jcde/qwad036]