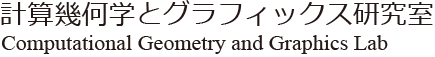Continuous Transforming of Crease Patterns of Twist Folding >JP

Abstract

Origami is anticipated to find applications as shrinkable and deployable mechanisms. In various fields such as aerospace engineering, medical engineering, and architecture, parametrically transformable origami models have been proposed to realize structures that meet specific conditions. This project proposes a parametric designing and transformation method for crease patterns named twist patterns, which is expected to be applied in such a way. The proposed method differs from existing methods exhibits a significant advantage in its capability to generate general flat-foldable. crease patterns. Therefore, the proposed method contributes to increased origami variations by transformations of existing crease patterns and to a unified discussion across disciplines.

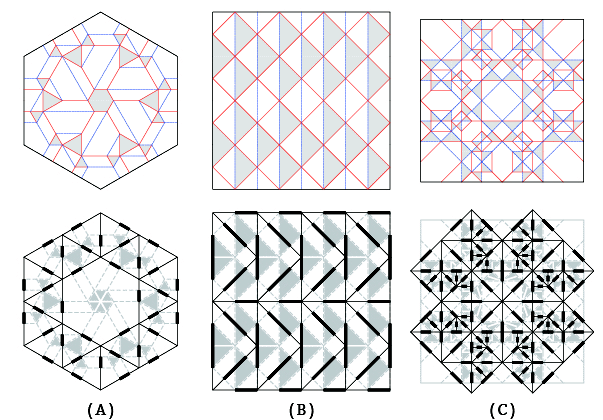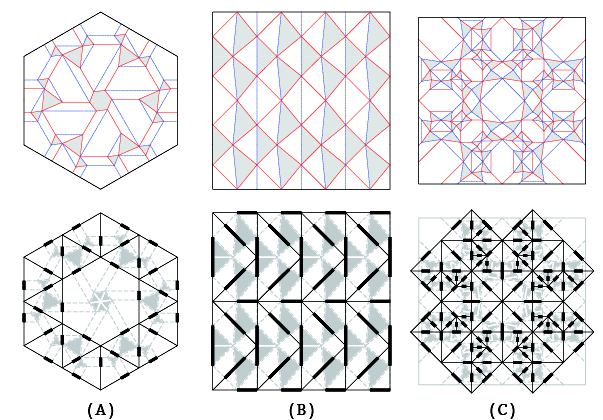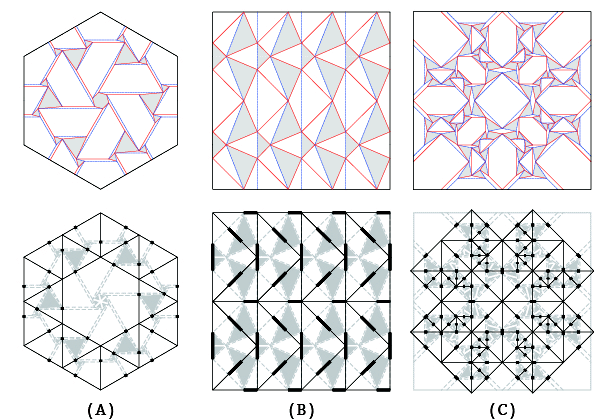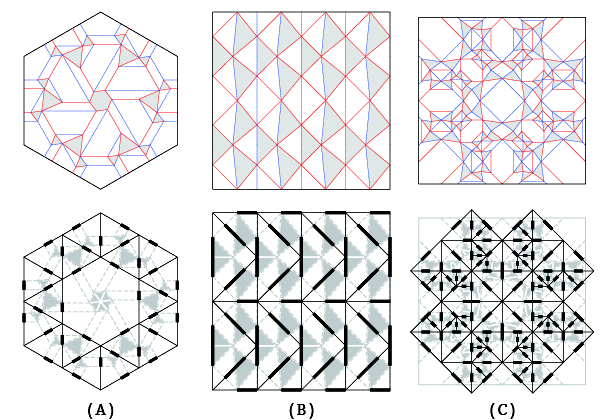
Fig.01.Example of parametric transformation with twist pattern as the unit
A:Roman Church Floor Tiling (designed by Eric Gjerde), B:Diamond pattern, C:Hydrangea (designed by Shuzo Fujimoto)

Index

Flat-Foldable Crease Patterns
Twist Patterns
Method to Design and Transform Twist Patterns
Method to interpreted crease pattern as twist patterns
Applied research
Achievements

Flat-Foldable Crease Patterns

(Flat-Foldable) Crease patterns in this project are a set of creases that satisfy the following rules (Fig.02)

The alternating sum of sector angles of an interior vertex must be 180°.
Creases connecting two points on the paper boundary are not included. (if included, they can be ignored.)
No need to distinguish between mountain and valley crease.

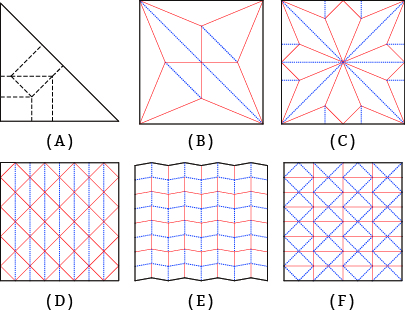
Fig.02 Examples of crease pattern
A:pattern for triangle twist fold, B:Bird base, C:Frog base, D:Yoshimura pattern (Diamond pattern), E:Miura-Ori, F:Watterbomb pattern

The set of facets resulting from the implementation of the following operations on a crease pattern is denoted as the folded state (Fig.03).

A spanning tree is constructed with all facets as nodes and creses between adjacent two faces as links
One facet is selected as the root (white dots in Fig.03A).
While traversing the spanning tree in order from the root, the leaf-side facets are all flipped over the crease corresponding to the link

Folded states have the following properties.

The set of facets coincides with a silhouette of the actual folded crease pattern.
The relative positions of the facets are uniquely decided no matter which facet is used as the root and no matter what graph the spanning tree is.

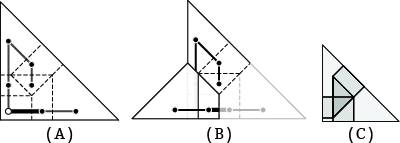
Fig.03 Flow of obtaining the folded state of Fig.02A
A:Spanning tree, B:Flipping facets about bold link in A, C:Folded state

Twist Patterns

Crease patterns consisting of creases that form a n-gon facet and parallel pairs of creases extending from the endpoint of the edge of the n-gon facet are refered (n-gon) twist patterns(Fig.04A)

Center facet: the central n-gon facet
Pleats：paralell pairs of creases
Pleat angles：Sector angle formed by each edge of center facet and pleat, which is on the counterclockwise side around the center facet

In an n-gon twist pattern, all n pleat angles are equal.
Twist patterns can be connected by sharing a pleat(Fig.04B).

When two creases overlap completely as a result of the connection, the pattern removing both is also the crease pattern.(Fig.04C)
The n-gon twist pattern can be regarded as multiple triangle twist patterns connected so that edges of their center facet are overlapped.(Fig.05).

In a twist pattern, and in the concatenation of them, folded states whose root is a facet surrounded by different pleats have each center facets rotated by twice the pleat angle.

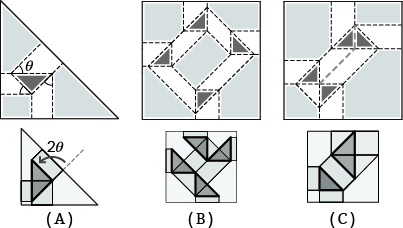
Fig.04. Example of twist patterns and their folded state whose root is one of the light gray facets surrounded by different pleats
A:Single triangle twist pattern, B:Connected four twist patterns, C:Connected twist patterns with overlapped creases

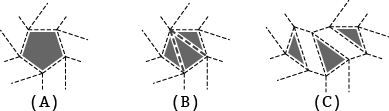
Fig.05. Single hexagon twist pattern interpreted as connected three triangle twist patterns
A:Single hexagon twist patter, B:Example of A with restored overlapped creases, C:Three triangle twist patterns with longer distance between center facets than B

Method to Design and Transform Twist Patterns

(Connected) Twist patterns can be generated by the following operations, which is called Twist pattern design method.

Placing a triangular tiling
For each tiling side, placing a segment, that is shortened by a common ration (and called pleat base), on a straight line along the side
For each pleat base, making two perpendicular creases (i.e., a pleat) through each endpoint
For each triangular tile, making a triangle facet (i.e., a center facet) by connecting the intersections of the pleats with creases
Triming the set of creases so that the pleats firing outward do not intersect (e.g., Trimming along the tiling boundary)

A set of generated twist patterns is (locally flat-foldable) crease pattern and have the following properties.

Inside creases may cross each other.( To prevent it, experiences of the design are needed.)
A triangle tile and its corresponding center facet are similar.
A set of connected triangle twist patterns can always be generated by this method.

A combination of tiling and pleat bases is referred to as a Guide.

Guides can be restored from the a set of connected triangle twist patterns by the reverse of the design method.
The Guides that are restored from a pattern are of innumerable types, since the position and size of the tiling can be freely determined.

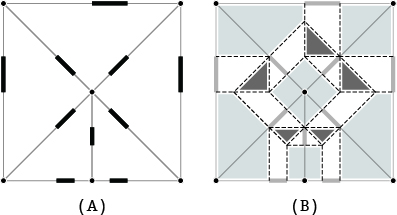
Fig.06.Twist pattern design method
A:Guide (Black blod lines are a pleat base), B:Generated set of connected twist patterns

By continuously transforming the following parametric elements of a Guide, the crease pattern can be continuously transformed.

Length of pleat base

To be precise, ratio of length to corresponding tile's edge common to all pleat bases

Position of pleat base (Fig.07)

To be precise, in the pleat base and corresponding tile's edge, ratio of the distances between their starting points and the distances their end points.
Each pleat base, with only its length altered, is positioned at location where this ratio remains unchanged.
A pleat base with zero-length is the origin of it.

Position of tile's vertex

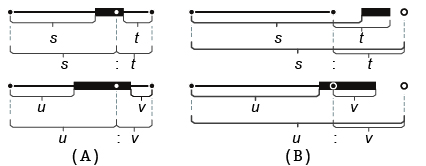
Fig.07. Doubling the length of pleat bases so that s:t=u:v and their origins (shown as white points)
A:Origin as internal division point of edge, B:Origin as external division point of edge

Before and after transforming only the length of the pleat base, the following holds.(Fig.08)

They have the same number of vertices and crease lines while keeping the connections between vertices (i.e., graph isomorphic)
Their facets surrounded by different pleats are only scalled.(The center of the scaling is the vertex shared by the edges of the guide　corresponding to the pleat surrounding the facet.)
Their center facets are sclled and rotated
In general, the property that creases do not cross is preserved.

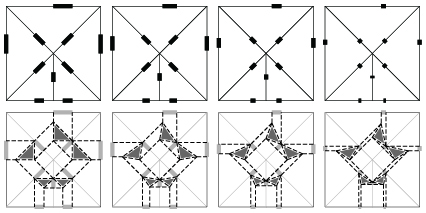
Fig.08. Crease pattern and its Guide in Fig. 6, and ones obtained by decreasing length of pleat base

Method to interpreted crease pattern as twist patterns

Interestingly, it is possible to generalize that flat-foldable crease patterns can be regarded as a set of connected triangle twist patterns.
In other words, twist patterns can be reconstructed from a crease pattern by following steps.

Obtaining the folded state from a given crease pattern(Fig.09A).
Classifying each facet into one of the following three types based on tha fact that each facet requires at most one flip or rotation and then at most one translation to coincide with its folded state.

Trans-facet: The facet that neither rotated nor flipped.
Rot-facet: The rotated facet.(Fig.09B)
Flip-facet: The flipped facet

From each Rot facet, reconstructing the following twist pattern with a central facet that has the same shape and rotation angle for coinciding with its folded state as the Rot facet(Fig.09C,10)

Center facet：The Rot facet
Pleat angles：Half of its rotation angle
Length of Pleat：Any length

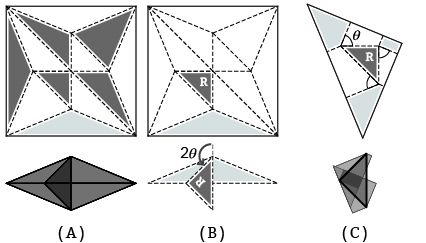
Fig.09.A:Bird base and its folded state(Trans facet(Light gray), Rot facet (Dark gray), Flip facet(White)),
B:One of Rot facet, C:Twist pattern reconstructed from B

Connecting twist patterns reconstructed from each Rot-facet, based on the following facts, as much as possible.(Fig10,11)

An edge of a rot-facet is always shared with a Flip-facet.
In a Flip facet, each Twist pattern, reconstructed from Rot-facets that share an edge of the Flip facet, fire a pleat at the same slope from the edge(Fig.10).
The reconstructed twist patterns can share a pleat with the twist patterns reconstructed on the opposite side of the Flip facet.

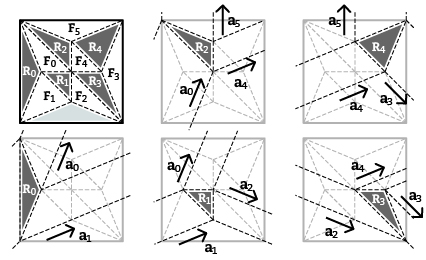
Fig.10. Twist patterns reconstructed from each Rot-facet R_i based on Fig.09A
a_i indicates the slope of the pleat, corresponding to the Flip face F_i

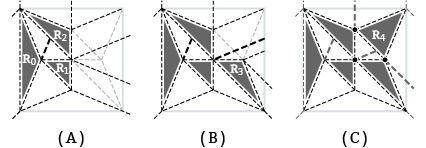
Fig.11.The process of connecting the five twist patterns in Fig. 10 (bold lines indicate overlapped creases))
A:Connecting Twist pattern of R₀,R₁ and R₂, respectively ,B:Connecting A and twist pattern of R₃,C:Connecting B and twist pattern of R₄

The set of reconstructed twist patterns, upon applying the following operations, coincides with the original crease pattern.

Removing overlapped creases
Define the same boundary as the original crease pattern
Removing creases connecting two points on the boundary

Folded states with a different facet as the root may reconstruct different a set of twist patterns(Fig.12)
In the folded state that have be rotated and flipped can also be used for reconstruction, in which case, there exist countless sets of twist patterns that can be reconstructed.

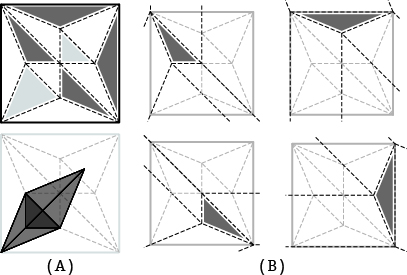
Fig.12. A:Folded states and Classified facets with a root different from Fig.A, B:Twist patterns reconstructed from each Rot-facet

Applied research

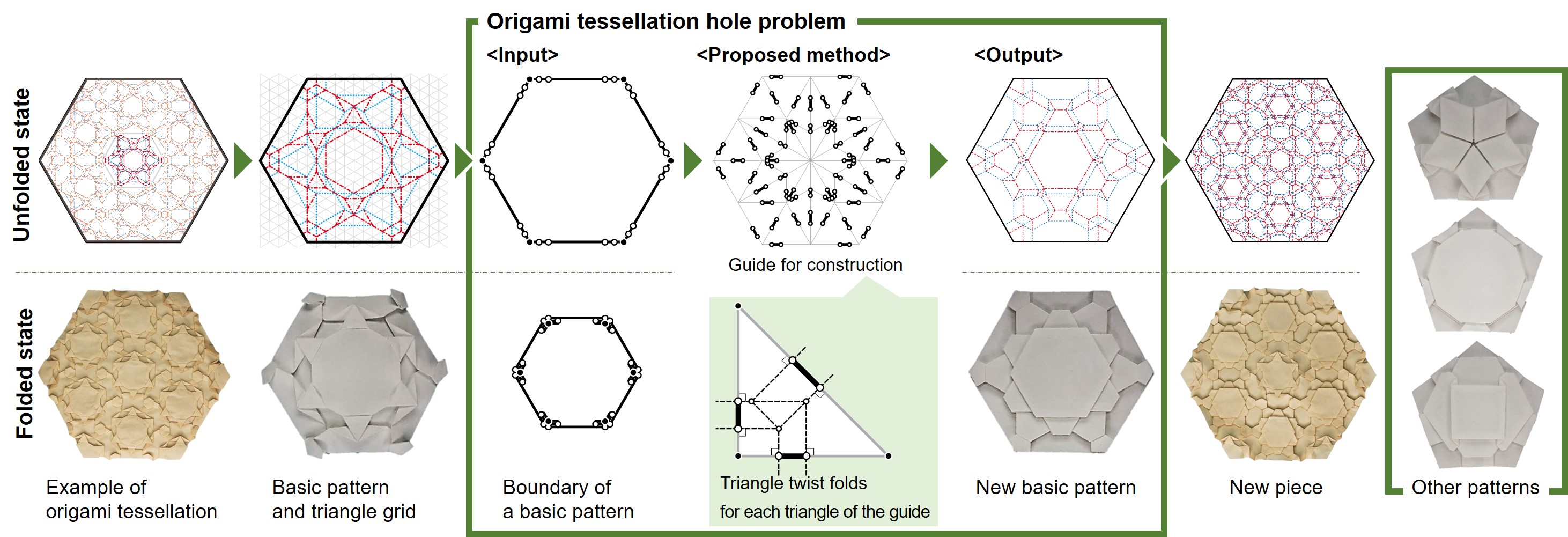
Method for solving origami tessellation hole problem using triangle twist folding[DOI:10.1093/jcde/qwab074]

Shrinkable Self-Similar Structure Design

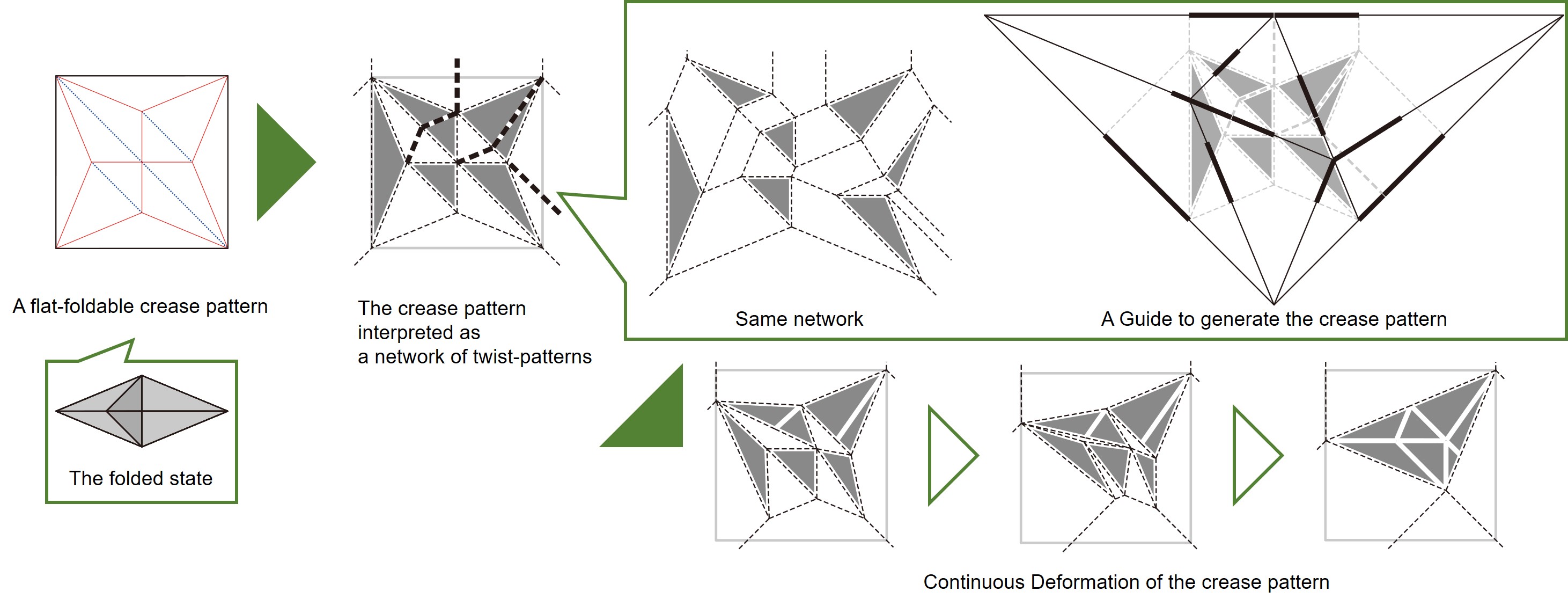
Continuous deformation of flat-foldable crease patterns via interpretation as set of twist-patterns[DOI:10.1093/jcde/qwad036]

Achievements

Academic papers (peer-reviewed)

Yohei Yamamoto, Riku Nakazato, Jun Mitani, "Method for solving origami tessellation hole problem using triangle twist folding", Journal of Computational Design and Engineering, Vol.9, No.1, , pp 144-154, 2022[DOI:10.1093/jcde/qwab074]
Yohei Yamamoto, Jun Mitani, "Shrinkable Self-Similar Structure Design", Journal of Mechanisms and Robotics, pp 1-10, 2022[DOI:10.1115/1.4053528]
Yohei Yamamoto, Jun Mitani, "Continuous deformation of flat-foldable crease patterns via interpretation as set of twist-patterns", Journal of Computational Design and Engineering, 2023[DOI:10.1093/jcde/qwad036]